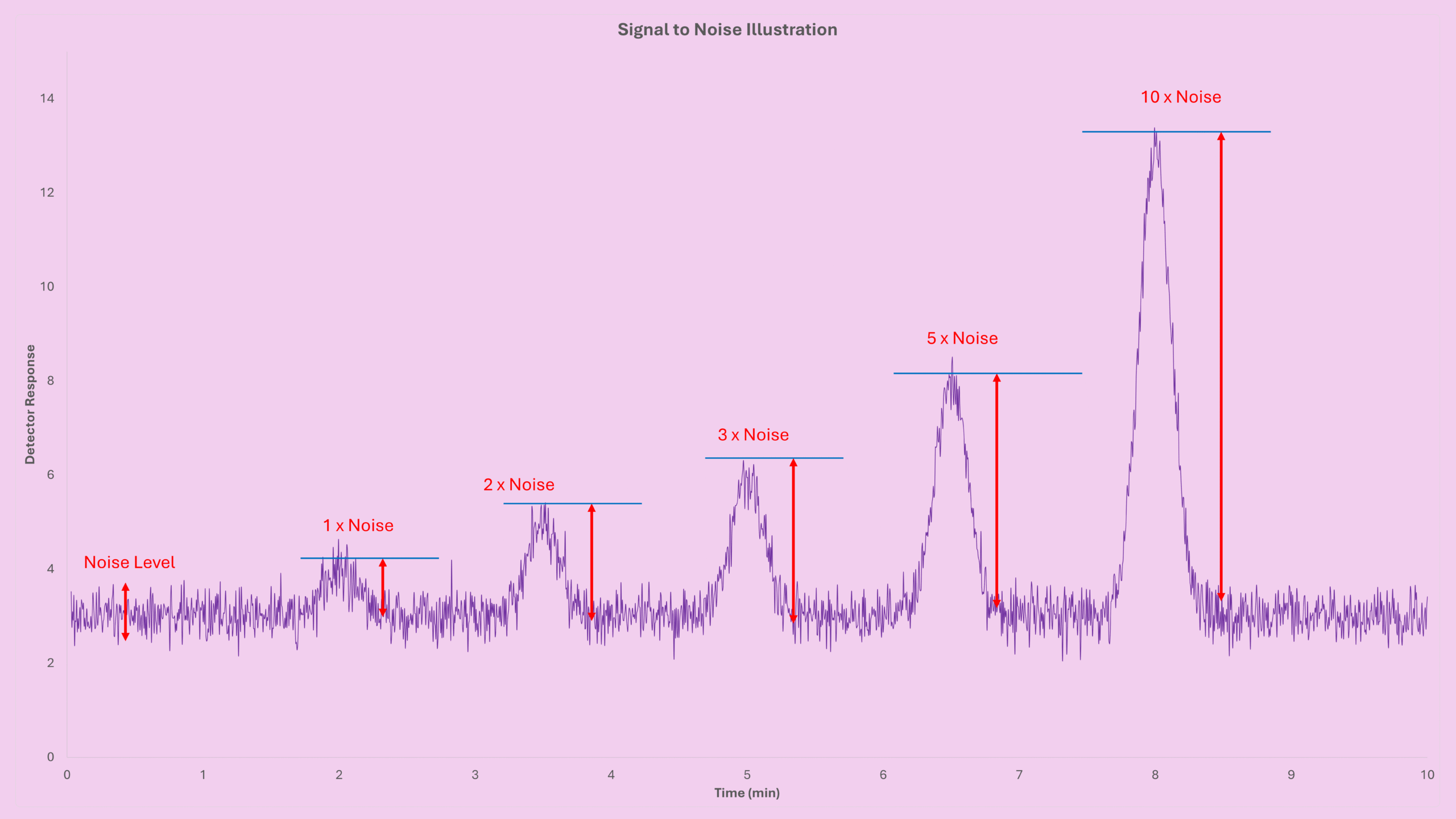
If you’ve been following along with my LOD series, you’ll remember the earlier post where I explained how to estimate LOD using the signal-to-noise ratio with peak height. In this new guide, we’ll take that foundation and extend it using the GC LOD formula based on peak area and peak width, which is another practical approach widely used by analysts. Since this method builds directly on the previous concept, I suggest reading that first GC LOD LOQ by Signal to Noise: A Friendly Guide for GC Users.
Understanding the GC LOD Formula (Peak Area Version)
The traditional height-based formula was:
LOD = (Factor × Noise × Concentration) / Height
However, many users find peak area more stable, especially when peak shape fluctuates slightly. That’s where this GC LOD formula comes in:
LOD = (Factor × Noise × Concentration × Width1/2 × 60) / Area
Let’s break down what each part means:
- Factor — typically 3× noise
- Noise — detector noise (peak-to-peak)
- Concentration — known concentration of the standard
- Width1/2 — peak width at half height (in minutes)
- 60 — converts minutes → seconds
- Area — peak area (for example pA*s in Agilent GC systems)
This formula looks slightly more complex, but once you understand where it comes from, it becomes straightforward.
Where the GC LOD Formula Comes From
Let’s start with the triangle-peak approximation. If your peak is symmetric — which is essential — the area can be estimated as:
Area = ½ × Full Width × Full Height
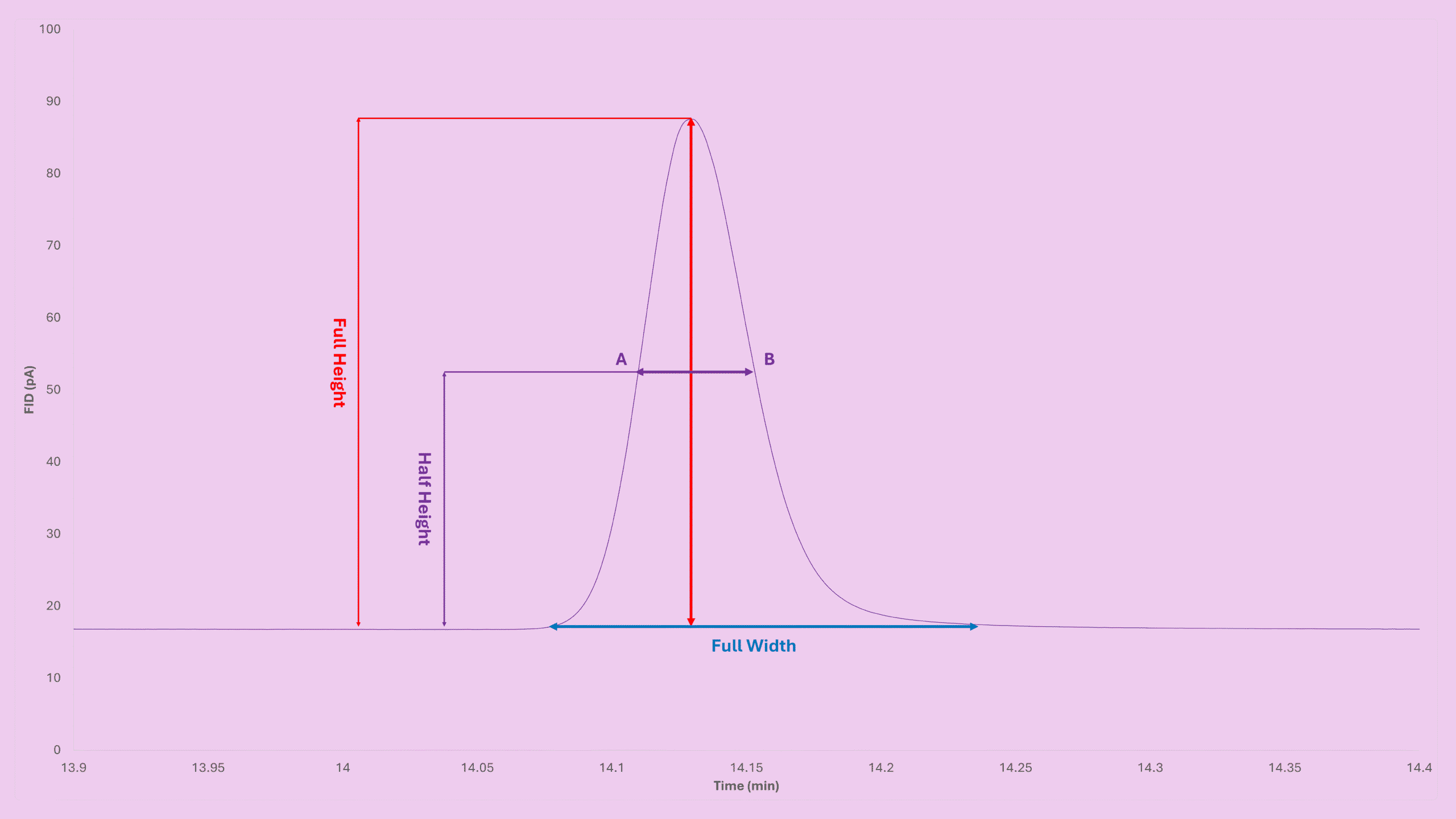
Because width1/2 is half of the full width for a symmetric peak, you get:
Area = Width1/2 × Height
But here’s the catch:
- Area in Agilent software = pA·s
- Width1/2 is in minutes
So we convert minutes to seconds:
Area = Width1/2 × 60 × Height
Rearranging:
Height = Area / (Width1/2 × 60)
Now plug this height into the original height-based LOD formula:
LOD = (Factor × Noise × Concentration) / Height
Becomes:
LOD = (Factor × Noise × Concentration × Width1/2 × 60) / Area
And that’s your complete LOD formula.
Where to Find Width1/2 and Area in Agilent GC Software
The Agilent software automatically calculates peak area and peak width at half height during integration.
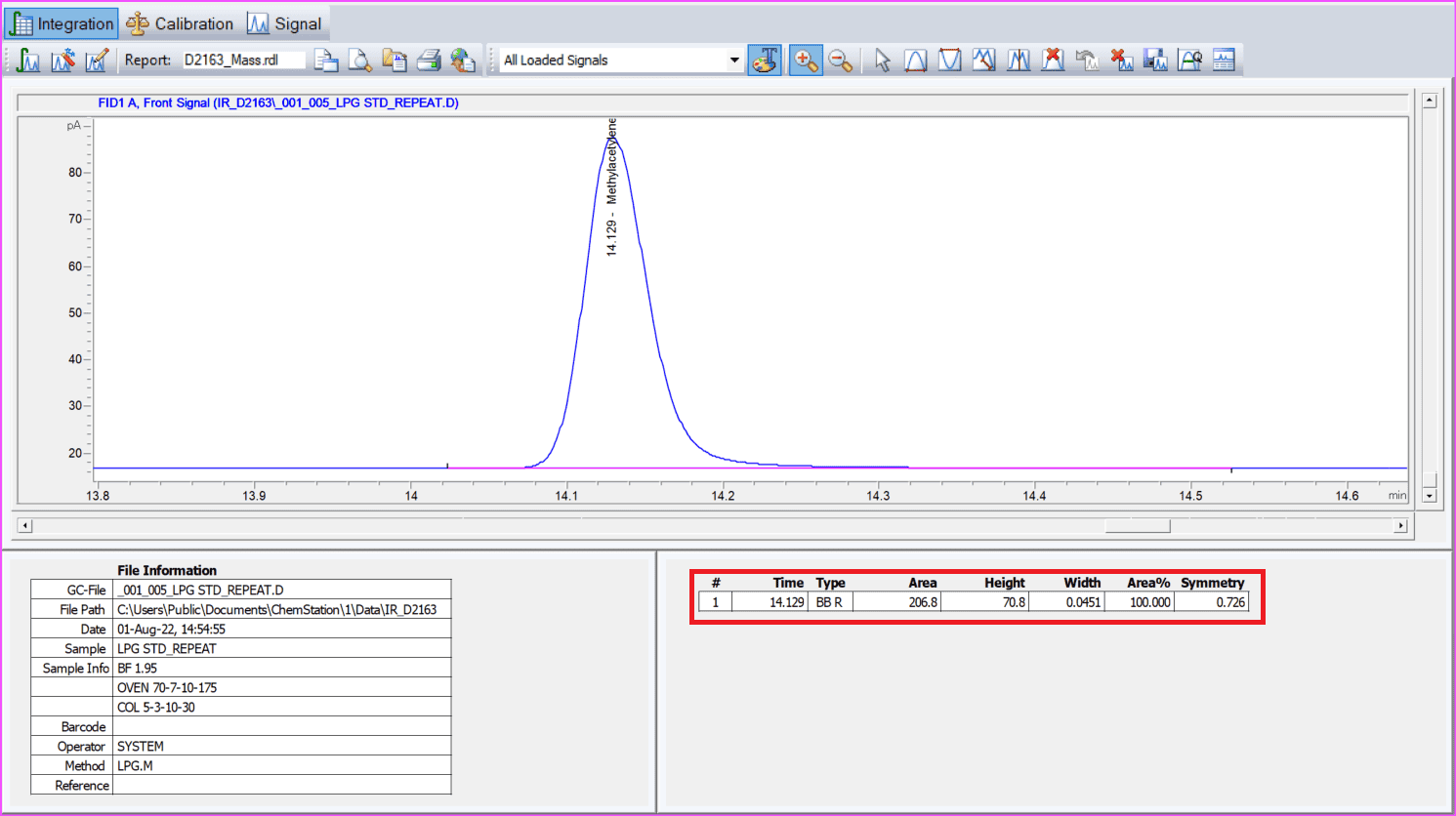
Look for the columns labeled Area and Width in the results table. The Width displayed is actually Width1/2.
If you use another GC platform, verify the units. The formula is correct only if:
- Area = detector units × seconds
- Width1/2 = minutes
Most Agilent software follows this standard.
LOQ from the GC LOD Formula
Once LOD is known, LOQ is simple:
LOQ = 3.3 × LOD
This comes from the typical assumption that LOQ = 10 × noise and LOD = 3 × noise.
Important Considerations When Using this GC LOD Formula
1. Keep Your Peak Symmetric
This method assumes a clean, triangular-like peak. Tailing or fronting affects accuracy.
2. Use a Standard Close to the True LOD
A simple guideline I often use:
- Standard / LOD < 10 → excellent
- 10–20 → acceptable
- >20 → risky
When possible, dilute your standard to bracket the expected LOD.
3. Units Must Match
Mixing platforms may change definitions of area and width.
4. LOD LOQ Units Follow the Standard
LOD LOQ always inherits the same units as your standard (ppm, mg/m³, µg/mL).
Key Takeaways
- The GC LOD formula using peak area provides a stable alternative to height-based LOD calculations.
- The core formula is:
LOD = (Factor × Noise × Concentration × Width1/2 × 60) / Area - Symmetry matters — always check peak shape.
- Agilent GC software conveniently displays both area and width1/2.
- LOQ is easily computed as 3.3 × LOD.
- A calculator is available at the top of the post for quick use.
Before You Go
If this explanation of the GC LOD formula helped clarify how peak width and area fit into LOD calculations, feel free to explore my full series about Detection Limit (LOD/LOQ) or check out the interactive GC LOD Calculator implementing this post approach . Each new post builds on practical, field-tested GC knowledge to help you work faster and with more confidence.
